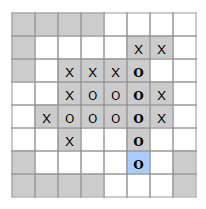
Noughts and crosses neural net version
Background
As you can see in my post "Beat my noughts and crosses game", the original plan was to use the game setting in order to play around with neural nets and to learn more about them. Now in the spring of 2016 I have finally taken the time to put all the pieces together and created a Neural Net that can play noughts and crosses. The only problem is that it does not seem to be able to beat my old rule based system (RB). The last version I created (N3) only beat the RB once every 10:th game or so. The previous two versions never succeeded to beat the RB. So to be fair, I did not fail completely. The Neural net actually manages to play. All be it not that well.
For code you need to look at the source of the samples. I have chosen not to show code in this post because it would be way too long. This is only to give you an idea of what kind of problem you are facing when working with machine learning.
Setup
Both the (RB) and (NX) system have the same access to knowledge about the board. Basically the get each playable position and four arrays one for each direction you can put an x or an o. I also calculate the score if my opponent plays this position in order to block that move if it is a good one. Let's call the arrays A, B, C and D. When each array is scored by the system it take the array with the highest score and returns it. It does not make that much of a difference if I use some other calculation. Because the calculations are the same for all systems. But it could of course make some difference when playing against a human. But currently I only want to compare different engines.
N1 the first version
Sample of the first draft - Be aware the network need some time to train at first...
I did not want the data set to be too big so I used the same data that my rule based system uses. I only look at one player at a time like this. ["", "", "o", "x", "?", "x", "", "", ""] => o:[0, 0, 1, 0, 0, 0, 0, 0] and x:[0, 0, 0, 1, 1, 0, 0, 0]. Now I can let the neural net calculate the score for setting an o or an x in the middle and return the sum of those scores.
Now I started out giving some samples to train the network on. basically [0, 0, 0, 0, 0, 0, 0, 0] with a score of zero and a combination of sets with four 1:s in a row with the score of 1, witch would produce a winning position. Then a set of three:s with a lower score and then two:s. One could perhaps call this a binary check. Only looking at one player at a time. But what if I have xooo?x. Then an o would be really good instead of the question mark. Because this logic does not take the opponent into account, blocking the fifth position rendering this move worthless. So after running this for a while I decide that I need to go bigger.
But before I expanded the array I also tried some reinforcement learning. I set the system up with a logger that logged each move of the two players. Then I added those moves to the training set before the next round and depending if the move belonged to a winner or a looser I would bump the training data up or down for that data point. This had the effect that the N1 got from random to an opponent that from time to time could give RB a small fight before loosing. But nothing more than that. One of the reasons is perhaps that it is not clear if a certain move is good or bad. Perhaps the network could have gotten better if I trained it more. Because after 100 matches we got about 400 features to train on. And my guess is that not all of those features had been well adjusted on the good vs. bad scale.
The sample from this section is a network with a training set from 100 matches.
N2 the second version
Sample of the second draft - Be aware the network need some time to train at first...
With the questions from the previous version in my head I set out to do a better version. This time I doubled the array so that I could show the network both players in the same data point like this ["", "", "o", "x", "?", "x", "", "", ""] => set:[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0]. Though I did play around some with the reinforcement learning I thought it would be good enough to have a fixed training set where I could specify some of the important positions that the network should know about. And then if I saw the network fail on some specific move I could enter some extra training data enhancing the network in that area. But that did not do much improvement. The reinforcement got way to many features and it was not clear if a move was good or bad, at least the way I had set it up. So I figured I needed to be more specific on what I wanted the network to know.
N3 the third version
They say that less is more. And that is true even here. Now I must admit that I am a bit disappointed that the neural network was not smarter than that... But in this attempt I focus on two things. The number of x or o there are in a row and how much remaining space there is. If the number of available slots are less than 5, then I can not get 5 in a row so even if there are 3 and I can put a fourth it is a dead end and I return the value zero. Using only these two values to train the network I could settle with a lot less features as you can see below.
// Training data N3
var input = [[0, 8], [1, 8], [2, 8], [3, 8], [4, 8], [5, 8], [0, 4], [1, 4], [2, 4], [3, 4], [4, 4], [5, 4]];
var desired = [[0],[0.06],[0.12],[0.25],[0.5],[1], [0],[0.03],[0.06],[0.12],[0.25],[0.5]];
The 8 ant the 4 is the amount of open positions. There can of course be a lot more variations on those. But here is where the beauty of neural nets com in and do a great estimation of what results should be given on those occasions. The thing is that if I do not train the network on the lower scores it does a pretty bad job as an opponent. But if you try it out it should actually be able to give you quite a match.
RB vs. N3
Let the battle begin RB as x and N3 as o
Now this is a bit annoying. I actually thought that the neural net would easily beat my rule based version. Primarily because there should be some holes in my list of rules that the network should be able to smooth out and by doing so win every match. But even though it is often quite a match and N3 does win from time to time, RB as x still turn out to be the winner most of the time.
Try to beat RB your self and see who you feel is the greater opponent.
Lessons learnt
I have not played around enough to rule out the neural net version of noughts and crosses and you might think that I lost a bit of faith in the neural net. But that is not the case. Neural nets are really good for a lot of things, but perhaps not such logic tasks as playing this simple game. They are great for more fuzzy areas where rules does not have the slightest chance to cover all the angles of a problem. This is where neural nets do a great job. No, I think in order to write a better xo game bot I will have to look more at the Minimax where you calculate a value from the state of the board and then you try to do some different steps let say we use our neural net to give us the 5 most promising moves and then we try those and see what moves the opponent can do, so that we get a tree of possible moves. Then we calculate the value of each end state and then set out to make the move that has the most promising outcome. And this is often how these machine learning techniques are used. You combine them to get the best out of each one until you find the most optimal decision or solution.
I also noticed that using a smaller net with just one hidden layer containing five nodes actually made the chance of winning a little bit higher than using two 10-node hidden layers. So one should not over do ones networks. The networks should probably reflect the size of the feature it has as input. But again, the size of the network only make a slight variation in the result in this case. The thing is that the network, regardless of size is always trained down to a certain small error. So the result should be basically the same regardless of how the network looks.
I also tried to use reinforcement learning on N3 but it just got worse and lost all games compared to winning 14 out of a hundred if I only used my predefined training sample.
Another interesting point to take home is that the RB is static so if I train the N3 so that it win once, I can use that state of the net to beat the RB every time. But then it would certainly be a boring game because the end state of the game would always look identical, because both players would always do the exact same moves. But since I'm retraining N3 before every game. It results in a different end state almost every time. So if you have a neural net that is trained it will not make different decisions when faced with the same problem. But if you retrain the network with the same training data you might end up with a slightly different game strategy that might be the winning kind.
So now that I have tried this and "succeeded" I'm ready to take on some new interesting challenges. I'll probably start to look at what tools are available out there to do these things and see how I can use them for more complex problems.
Findings after some more play
After playing around for a while more I came to the conclusion that real numbers might not be ideal for the neural net. So I changed the input to [n1, n2, n3, n4, n5, m] where n1 is 1 if there is 1 x and both n1 and n2 if there are 2 x in a row and so on. The m only tells the net if there is room for 5 x in a row or not. When doing this and updating the training data I could get the N5 to beat the RB 85% of the time. The solution always seem to be the same when winning and a few variations when loosing. But then again, beating the RB might only be that the N5 has found a whole in the rules.
Another issue with the N5 solution is that it has training data for every possible feature that I can have. So basically I could just ignore the neural net and just return the values I use as training data. So when I think of it I have just created another rule based system... But here is an interesting point that should prove the value of neural nets in other situations. If I remove almost all training data and only train the network with the extreme values, the winning state and the complete opposite then the network can still play a decent game of noughts and crosses. Even though it looses every time when playing the RB (See N5b).
// Complete set of training data for N5
var input = [
[0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0],
[1, 1, 1, 1, 0, 0],
[1, 0, 0, 0, 0, 1],
[1, 1, 0, 0, 0, 1],
[1, 1, 1, 0, 0, 1],
[1, 1, 1, 1, 0, 1],
[1, 1, 1, 1, 1, 1],
];
var desired = [
[0],
[0],
[0],
[0],
[0],
[0],
[0.05],
[0.4],
[0.7],
[1.0],
];
// N5b has less training data but still can play
var input = [
[0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1],
];
var desired = [
[0],
[1],
];
Try to beat the N5 or see the N5 battle the RB. If you want to see the results, then activate the console by pressing F12 and click the console tab. (There also is an N4 that pushed the winning strike up to about 40% at best.)
- ai, javascript, game, software